Filters on data
Lowpass filter
Digital
EWMA
A specific variant of a moving average, the exponentially weighed moving average (EWMA) (also exponential moving average, EMA) is an easy-to-realize (first-order) lowpass on discrete time-domain data.
Intuitively, you create an output that adjusts only slowly to new values.
That implicitly meaning it responds more sluggishly to quick changes (high-frequency content) so mostly follows the overall tendency of the signal (lower-frequency content).
The influence of older data points reduces quickly (works out as exponentially decaying, hence the name), though it never quite reaches zero, which is part of why it is technically a (first-order) infinite impulse response filter(verify) (though in most computer implementations it actually does reach zero effect, because of floating point reality, this is a footnote).
There is a parameter α to vary its sensitivity (typically a small value)
- In cases of not-so-regular sampling, α is related only to speed of adaptation to newly sampled values
- It's still relevant to frequency content, but not in a particularly quantifiable way
- In applications that sample at a regular interval, you can relate α directly to frequency content.
- For example sound. Also e.g. some sensor systems, where it's optional, but this filter can sometimes be be more meaningful this way.
When you want to calculate a filtered output series from an input series, you can loop through a list doing something like:
filtered_output[i] = α*raw_input[i] + (1-α)*filtered_output[i-1]
...or the equivalent:
filtered_output[i] = filtered_output[i-1] + α*(raw_input[i]-filtered_output[i-1])
The latter form may feel more intuitive/informative: the change in the filtered output is proportional to the amount of change, and to to the filter strength α.
Both may help consider how using the recent filtered output gives the system a sort of inertia:
- A smaller α (larger 1-α in the former) (also makes for larger RC) means the output will adjust more sluggishly, and should show less noise (since the cutoff frequency is lower(verify)).
- A larger α (smaller 1-α) (smaller RC) means that the output will adjust faster (have less inertia), but be more sensitive to noise (since the cutoff frequency is higher(verify))
Since the calculation is local and in one direction, you can choose to keep only the latest value. This make sense e.g. when your primarily goal is presenting a filtered version of a noisy or crude sensor
current_output = α*current_input + (1-α)*previous_output previous_output = current_output
You often want implement the above in floating point, even if you return ints, to avoid problems caused by rounding errors.
- Most of the problem: when alpha*difference (itself a floating multiplication) is less than 1, it becomes 0 in a (truncating) cast to an integer.
- For example, when alpha is 0.01, then a signal differences smaller than 100 will make for an adjustment of 0 (via integer truncation), so the filter would never adjust particularly close to the actual value.
- You can do it in pure integer, it just takes more implementation care
Graphical example
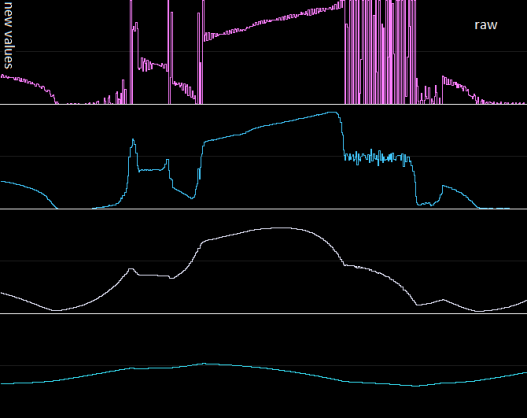
The top signal is the raw input (a few seconds's worth of an ADC sampling from a floating pin, with a finger touching it every now and then, e.g. picking up 50Hz).
The ones below are EWMA'd versions of it, at increasing strengths.
Some observations:
- the suppression of fast peaks and deviations
- it is certainly possible to filter too hard - see the fourth one down, and probably the third as well. Depends on your purpose and what you're sampling, really.
- the filter is proportional to the difference, so initially fast, then slower and slower, sort of asymptotic to the real value
- introduces a shape like a charging capacitor (most visible in the third one down)
- it won't quickly saturate to the minimum or maximum of the range
- the filtered version of the the full-range oscillation comes out halfway not so much because of filtering, but also largely because most raw samples around there are effectively saturated at both ends of the ADC's numeric range. (This is essentially false signal - clipping, i.e. distortion)
On α, τ, and the cutoff frequency
α is the smoothing factor, theoretically between 0.0 and 1.0.
In practice typically <0.2 and often <0.1 or smaller, because above that you're barely doing any filtering (or sampling verrrry slowly).
In applications with relatively regular sampling, α is often based on:
- Δt (dt), the time interval between samples (reciprocal of sampling rate)
- a choice of time constant τ (tau), a.k.a. RC
- (RC latter seems a reference to a resistor-and-capacitor circuit, which does lowpass in much the same way. Specifically, RC gives the time in which the capacitor charges to ~63% of the potential difference[1])(verify)
Specifically:
α = dt / (RC + dt)
In practice you'll often choose an RC that is at least a few multiples of dt, which means that α is on the order of 0.1 or less. (if using an RC close to dt you'll get alphas higher than ~0.5, which barely does anything)
In applications with strictly regular sampling interval (e.g. for sound), RC's relation to frequency content is well defined.
For example, the knee frequency (where it starts falling off, approximately the cutoff frequency) is:
1 / (2*pi*RC)
For example
- when RC=0.002sec, the knee/cutoff is at ~80Hz.
- at 200Hz, 2000Hz, and 20000Hz sampling, that makes for alphas of 0.7, 0.2, and 0.024, respectively.
(At the same sampling speed: the lower alpha is, the slower the adaptation to new values, and the lower the effective cutoff frequency)(verify)
For a first-order lowpass:
- at lower frequencies, the response is almost completely flat,
- at this knee frequency the response is -3dB (has started declining in a soft bend/knee)
- at higher frequencies it it drops at 6db/octave (=20dB/decade)
(Higher-order variations fall off faster and have a harder knee)
Note there will also be a phase shift, which lags behind the input.
It depends on the frequency; it starts earlier than the amplitude falloff, and will be -45 degrees at the knee frequency(verify).
Arduino example
Note: This is a single-piece-of-memory version, for when you're interested only in the (latest) output value, e.g. smoothing noisy sensor output.
// keeps values for each analog pin, assuming a basic arduino that muxes 6 pins.
// you can save a handful of bytes of RAM by putting your sensors on lower-numbered pins and lowering...
#define LOWPASS_ANALOG_PIN_AMT 6
float lowpass_prev_out[LOWPASS_ANALOG_PIN_AMT],
lowpass_cur_out[LOWPASS_ANALOG_PIN_AMT];
int lowpass_input[LOWPASS_ANALOG_PIN_AMT];
int adcsample_and_lowpass(int pin, int sample_rate, int samples, float alpha, char use_previous) {
// pin: arduino analog pin number to sample on (should be < LOWPASS_ANALOG_PIN_AMT)
// sample_rate: approximate rate to sample at (less than ~9000 for default ADC settings)
// samples: how many samples to take in this call (>1 if you want smoother results)
// alpha: lowpass alpha
// use_previous: If true, we continue adjusting from the most recent output value.
// If false, we do one extra analogRead here to prime the value.
// On noisy signals this non-priming value can be misleading,
// and with few samples per call it may not quite adjust to a realistic value.
// If you want to continue with the value we saw last -- which is most valid when the
// value is not expected to change significantly between calls, you can use true.
// You may still want one initial sampling, possibly in setup(), to start from something real.
float one_minus_alpha = 1.0-alpha;
int micro_delay=max(100, (1000000/sample_rate) - 160); // 160 being our estimate of how long a loop takes
//(~110us for analogRead at the default ~9ksample/sec, +50 grasped from thin air (TODO: test)
if (!use_previous) {
//prime with a real value (instead of letting it adjust from the value in the arrays)
lowpass_input[pin] = analogRead(pin);
lowpass_prev_out[pin]=lowpass_input[pin];
}
//Do the amount of samples, and lowpass along the way
int i;
for (i=samples;i>0;i--) {
delayMicroseconds(micro_delay);
lowpass_input[pin] = analogRead(pin);
lowpass_cur_out[pin] = alpha*lowpass_input[pin] + one_minus_alpha*lowpass_prev_out[pin];
lowpass_prev_out[pin] = lowpass_cur_out[pin];
}
return lowpass_cur_out[pin];
}
void setup() {
Serial.begin(115200);
//get an initial gauge on the pin. Assume it may do some initial weirdness so take some time
// Takes approx 300ms (300 samples at approx 1000 samples/sec)
adcsample_and_lowpass(0, // sample A0 pin
1000, // aim for 1000Hz sampling
300, // do 300 samples. Should prime the value to something real, so that the loop code doesn't have to think about this
0.015, // alpha
false); // first sample is a set, not an adaptation
}
void loop() {
// updates can often be shorter (consider maximum adaptation speed to large changes, though)
int resulting_value = adcsample_and_lowpass(0, // sample A0 pin
1000, // aim for 1000Hz sampling
50, // follow 50 new samples
0.015, // alpha
true); // adapt from stored value for this pin (settled in setup())
Serial.println(resulting_value);
}
Semi-sorted
Aliasing and oversampling
See also
- http://en.wikipedia.org/wiki/Low-pass_filter#Algorithmic_implementation
- http://en.wikipedia.org/wiki/Moving_average#Exponential_moving_average
- http://en.wikipedia.org/wiki/Exponential_smoothing#The_exponential_moving_average
Other filters you can use include:
Analog
RC filter
Hampel filter